Come si impara alle elementari, un numero primo è divisibile soltanto per 1 e per sé stesso. A parte il 2, sono tutti dispari e separati da una certa distanza gli uni dagli altri, se si eccettuano i cosiddetti numeri primi gemelli, come l’11 e il 13, separati soltanto da un numero pari. Due di questi numeri gemelli sono citati nel romanzo, poi diventato film, La solitudine dei numeri primi, di Paolo Giordano, dove i protagonisti sembrano avvicinarsi ma non arrivano mai a toccarsi.
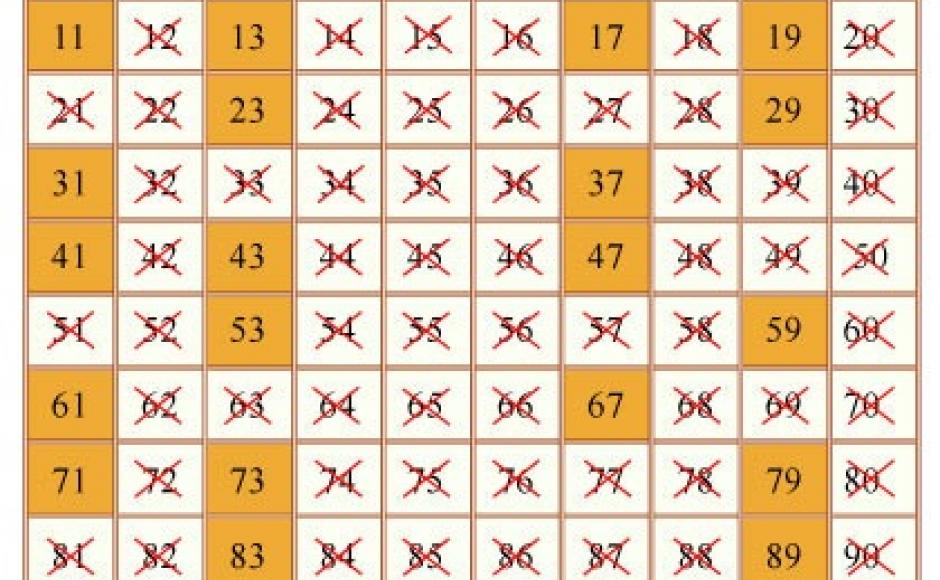
Un metodo pratico insegnato nella scuola primaria per individuare i numeri primi è il cosiddetto setaccio o crivello, che consiste nello scrivere ordinatamente i numeri in una tabella, per esempio da 1 a 100, e nell’eliminare tutti i numeri che non sono primi con il seguente metodo: si cancellano tutti i multipli del 2, escluso il 2, poi del 3, a eccezione del 3, e così via, ricominciando ogni volta dal numero successivo che non è stato cancellato, fino a che non restano che i numeri primi.
Questa procedura fu inventata intorno al 240 a.C. dal matematico greco Eratostene di Cirene. In linea puramente teorica, il metodo si può utilizzare per trovare numeri primi sempre più grandi, scontrandosi però ovviamente con l’insormontabile difficoltà di avere a che fare con una quantità enorme di numeri da maneggiare. Si è pensato di mettere in pratica la procedura utilizzando i computer, tuttavia anche la memoria dei calcolatori più moderni risulta troppo limitata per portare a termine tutti i calcoli necessari: si pensi che soltanto per calcolare tutti i numeri primi fino a mille miliardi è necessaria una memoria di un miliardo di byte
Il crivello di Eratostene, sviluppato più di duemila anni fa, è utilizzato anche nella codifica crittografica delle informazioni in modo sicuro, per esempio per gli acquisti on-line o per le transazioni bancarie, alla cui base c’è una tecnica che esprime ogni numero come prodotto di numeri primi.