Nelle sue opere Euclide espose i fondamenti della geometria sotto forma di verità assolute (assiomi, o postulati) dalle quali far derivare le altre proposizioni. Euclide propose cinque postulati, tutti immediatamente evidenti e verificabili, a parte l’ultimo.
Il quinto postulato (o postulato delle parallele) stabilisce che per un punto non appartenente a una retta passa una e una sola retta parallela alla retta data. Gli altri quattro assiomi affermano, nell’ordine, che: 1) per due punti distinti passa una retta; 2) ogni segmento si può prolungare indefinitamente; 3) si può tracciare, su un dato piano, una circonferenza di centro e raggi arbitrari: 4) tutti gli angoli retti sono uguali.
Se si analizzano con attenzione i primi quattro postulati si nota che si riferiscono a porzioni limitate di rette e piani e sono pertanto facilmente verificabili, mentre per il postulato delle parallele la verifica andrebbe fatta su una distanza infinita.
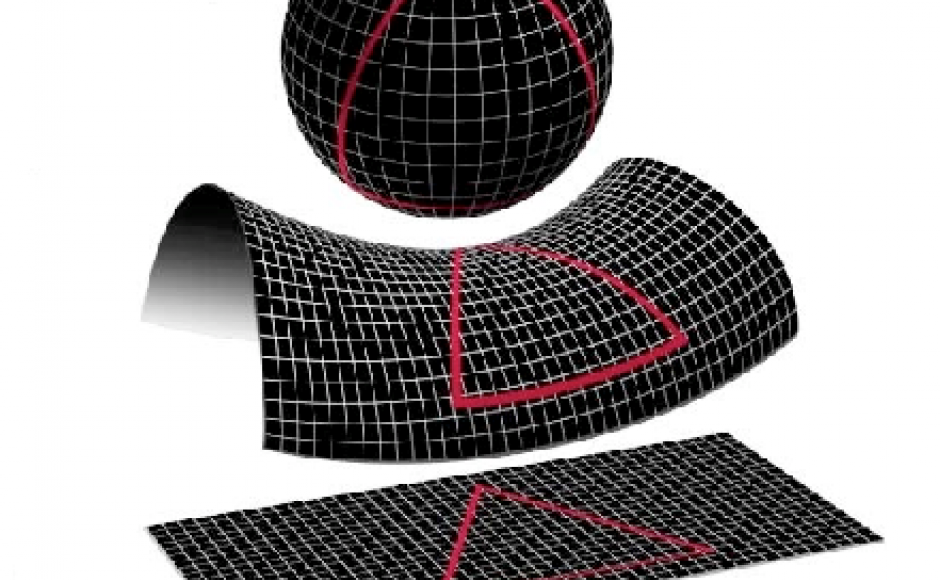
Per secoli si è tentato di far derivare il postulato delle parallele dagli altri quattro, ma invano, e nel 19° secolo è stata dimostrata la sua indipendenza, che ha portato alla conclusione che oltre alla geometria euclidea ne esistono altre in cui il postulato non vale, e precisamente quella nella quale da ogni punto escono infinite parallele a una retta data (geometria iperbolica) e quella in cui non esistono parallele (geometria ellittica). Prendendo in considerazione la familiare figura del triangolo, nella geometria euclidea la somma dei suoi angoli interni vale 180° (in basso nella figura), nella iperbolica è minore di 180° (al centro) e in quella ellittica è maggiore di 180° (in alto).
Esaminiamo ora lo spazio-tempo dell’Universo: in base alla teoria della relatività generale di Einstein, esso è localmente descritto da una geometria ellittica, con la curvatura determinata dalla presenza di materia. Per quanto riguarda l’Universo nel suo insieme, nessuna decisione può essere presa sperimentalmente. Per distanze di pochi milioni di chilometri le tre geometrie si equivalgono e la scelta di adottarne una piuttosto che un’altra è del tutto convenzionale e ricade sulla quella euclidea, peraltro ipotizzata dalle attuali osservazioni, perché più facilmente trattabile.